"Functional Programming Matters" in Scala,Haskell,and Java8
This workshops is based on the paper from 1984 (1990 revision) Why Functional Programming Matters written by John Hughes.
It is fascinating that this old paper was originally written when many of current programmers were not even planned by their parents and still it seems like it was inspired by current technological discussions.
In the introduction part author describes actually brilliant observation that you can not convince people to use certain programming language just by forbidding usage of some mechanisms from other languages.
So in the second part of the paper we can see many examples how functional composition, high order functions and lazy evaluation really simplify composition in computer programs.
Scala,Haskell,Java8
In the paper some abstract mathematical examples were used by Author to demonstrate advantages of FP. This abstract language has syntax similar to Haskell because it perfectly shows
To maximize "learning experience" this workshop is only inspired by the original paper but doesn't copying all examples line by line. So the main language in exercises will be Scala which has many powerful FP features and also its popularity raises chance that participants may actually use it in production.
Then we compare our solutions to Haskell which is pure functional language and if you write something in it then it should be ... yes, purely functional. And Finally we solve some exercise in java8 which has some primitive functional mechanisms but it is commonly known language so people should find many references to their daily work.

About glue and composition
In the first part we are going to practice functional composition. We can say that two programs compose when we can combine two pieces of code without additional "glue" like ifs,loops or additional exception handling.
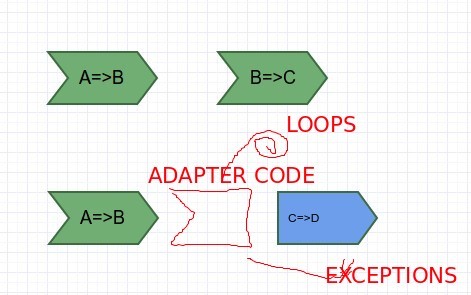
Two pure functions compose when second one receives as an argument type returned by the first one. There is a lot material on net explaining when function is "pure" so here we will only mention that when for given x we have always the same y then there should be no dependency on the outside mutable state and computations are pure.
In Scala we can compose functions with operator andThen or compose
val getPrice: Product => BigDecimal = p => p.price
val gross: BigDecimal => BigDecimal = net => net * 1.23
val display: BigDecimal => String = price => s"$price PLN"
//composition without additional glue
val displayGross: Product => String = getPrice andThen gross andThen display
val displayGrossCompose: Product => String = display compose gross compose getPrice
We saw how to compose simple functions. Now - inspired by the paper - we are going to check so called high order function foldr.
This is where knowledge of Haskell is very convenient because we can easily check this function type.
> :t foldr
foldr :: Foldable t => (a -> b -> b) -> b -> t a -> b
-- explanation
-- foldr :: Foldable t => (foldableFunction) -> zero -> inputList -> result
- So for example this type "(a -> b -> b)" in case of joining list of integers into string will have a specific types "Int->String->String".
- and now we could easily compose another Int->Int function in front of the foldr
However this will not work out of the box in scala because List.foldr receives actually two argument function (a,b)->c. Fortunatelly there are predefined operators to change (a,b)->c into a->b->c and the other way around. Moreover we will implement those functions by ourselves as an exercise during workshops (more theory : https://pl.wikipedia.org/wiki/Currying).
And by the way - this is good time to jump from theory into practice.
Exercises
Scala
- train basic composition,currying and basic usage of high order functions
Java8
- The same exercises as in scala
Haskell
- In Haskell file there are some examples to play with in GHCi console. And couple exercises with "by hand assertions". In subpages of this section you can find solutions.
High Order Functions
Let's return for a moment to the foldr function in Haskell. It has a type :
> :t foldr
foldr :: Foldable t => (a -> b -> b) -> b -> t a -> b
So the function (a->b->b) is the first parameter. In Scala we also have foldr avilable on collections however because of OOP approach first argument is actually reference to an object.

This is not only a cosmetic difference because Scala choice simplifies type interference but unfortunately the cost is in loosing high order function composition.
That's why -at first - we are going to create general high order function loop in Scala way :
def generalLoop[A, B](l: List[A])(zero: B)(f: (A, B) => B): B = l match {
case Nil => zero
case head :: tail => f(head, generalLoop(tail)(zero)(f))
}
and later in exercises we will create second definition in Haskell way :
def customFoldR[A, B](f: (A, B) => B)(zero: B)(l: List[A]): B = l match {
case Nil => zero
case head :: tail => f(head, customFoldR(f)(zero)(tail))
}
Exercises
Scala
- create custom curry,uncurry
- create foldr in Haskell way
- use foldr to define other High Order Functions
- similar exercises to those in scala section
Haskell
- In Haskell Part we will see some examples of High Order Functions in Haskell and we will create custom map and filter with foldr
Laziness
Last mechanism mentioned in the paper "Why Functional Programming Matters" is called Lazy Evaluation. In the paper author shew an example on how imperative loop can be completely replaced by infinite stream of values.
Because of laziness "infinity" cost us nothing (because nothing is executed) and moreover we can modify this stream of values with simple and high order functions described in previous sections.
Scala is an eager language by default but has dedicated Stream mechanism to work with lazy computation.
It can be created like a simple list :
val stream: Stream[Int] = 1 #:: 2 #:: 3 #:: Stream.empty
but also we can use general description of computations which will be represented by stream
val fromOne: Stream[Int] = Stream.from(1) //1,2,3...
Stream.iterate(1)(_+2) //1,2,5,7...
Stream.iterate(1)(_*2) //2,4,8,16...

Streams can be not only recursive but also interact with itself so we can use in computation previous and next value in the same time. This way we can define very readable - stack safe - Fibonacci sequence.
let fib = 0 : 1 : zipWith (+) fib (tail fib)
It also give us possibility to compute square root with Newton Method which calculates square root with provided approximation.
In this final example we will use all mechanisms practiced during workshops.
Exercises
Scala
- work with lazy streams
- compute FizzBuzz
- find prime numbers without loops
Java8
- Java8 introduced Streams. We will use this framework to work with infinite data streams
Haskell
- We are going to experiment with Haskell "laziness by default" and see solution to oryginal square root problem from the paper.
Additional Links
- Scala Streams in practice : http://blog.dmitryleskov.com/programming/scala/stream-hygiene-i-avoiding-memory-leaks/