Workshop - Pattern Matching & Algebraic Data Types

During these classes we are going to learn how to decompose data instances with pattern matching, why this process doesn't break encapsulation and how it helps to write total function to prevent a whole set of potential bugs which appears when we are using partial function as it was total function.

Let's start!

Pattern Matching Syntax

We are going to start our education by taking closer look at pattern matching syntax in Scala.

Basic example of PM is shown below.

someValue match{
        case 1 => //value or action for case 1
        case 5 => // value or action for case 5
}

Take look at the LAB FILE : https://github.com/PawelWlodarski/workshops/blob/master/src/main/scala/jug/lodz/workshops/fppatternmatching/exercises/PMPart1Syntax.scala

In the Demonstration part you can find following examples :

  • matching on a simple value
  • matching on a simple value with "default case"
  • using matched value in further processing
  • Pattern Matching on list

Exercises

Exercise for this section are grouped in three levels:

Exercise : Level 1 - basic syntax

  • ex11 - Match on concrete value
  • ex12 - define a function which maps given Int into String "even" or "odd"

so 

//List(1,2) changes into List("odd","even")

Exercise : Level 2 - matching lists

  • ex21 : return first element of List[Int] or zero if list is empty
  • ex22 : revert list but only if list has three elements

so 

//List('a','b','c') changes into List('c','b','a')

Exercise : Level 3 - PM with recursion

  • ex 31 : calculate list size
  • ex 32 : return last element of a list or None if list is empty

Take notice that method should return Option[A]

def lastElement[A](list:List[A]):Option[A] = ???

Matching on Case Classes

We have mastered pattern matching on simple types - now it's time for case classes which often represents more sophisticated domain objects.

LAB FILE : https://github.com/PawelWlodarski/workshops/blob/master/src/main/scala/jug/lodz/workshops/fppatternmatching/exercises/PMPart2CaseClasses.scala

In the demonstration part you can check :

  • How to decompose case class : OuterClass(InnerClass(value)) => value
  • How to keep reference to decomposed class : reference @ OuterClass(InnerClass(value)) => s"this is $reference"
  • How to ignore some case class properties when we don't need them in PM
  • How to match a List of Case classes
  • How to use Pattern Matching in List mapping

Exercises

Exercise for this section are grouped in three levels:

Exercise : Level 1 - simple wrapper

  • ex 11 : extract value from single wrapper
  • ex 12 : extract values from List of wrappers

Exercise : Level 2 - complex object

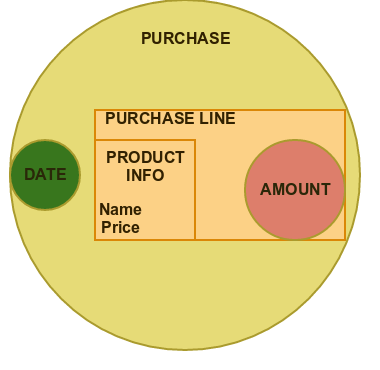
  • ex 21 : extract dates from List of purchases
  • ex 22 : Each Purchase contains of couple PurchaseLines which has price field. calcualte sum of all prices from given purchase.
  • ex 23 : Create List of pairs [date,sum of prices from this date]. Assume that you have only two purchases made in different days.

Exercise : Level 3 - modeling server

  • ex 31 : create function which imitate web server :

    • Match on case where you receive GET request - and then check if given page is available in web Map.
    • Match on case where other methods were used (POST,PUT etc.)

  • ex 32 : create mapper over request

Function is called converter: 

def converter[A, B](ra: Request[A])(f: A => B): Request[B] = ???

Implement this function with Pattern Matching. Does this function signature looks somehow familiar?

Algebraic Data Types

After mastering Pattern Matching with primitive and compound values - it's time to take closer look at a new idea of defining data which makes pattern matching very useful.

What is Algebraic Data Type?

Let's imagine an abstract data concept with limited number of possible values

  • Boolean : True & False
  • Day : Monday or Tuesday or Wednesday or Thursday or Friday or Saturday or Sunday
  • RequestMethod : GET or HEAD or POST or PUT or DELETE or TRACE or OPTIONS or CONNECT or PATH
  • UserRole : ADMIN or CONSUMER or CONSULTANT

But values don't need to be just simple values - they can be parameterized by additional parameters. So if you take a look from another angle you may find new meaning for a concept of constructor

  • Option : Some(value) or None
  • Try : Success(value) or Failure(error)
  • Shape : Circle(x,y,radius) or Square(x1,y1,x2,y2)

Values Can be Recursive

  • Expression : Number(value) or Add(Expression,Expression)
  • List : Cons(head,List) or Nil

How to implement ADT?

LAB FILE : https://github.com/PawelWlodarski/workshops/blob/master/src/main/scala/jug/lodz/workshops/fppatternmatching/exercises/PMPart3ADTs.scala

So this data can be implemented as an enum but Scala offers other mechanism better integrated with pattern matching.

sealed trait BOOLEAN
case class TRUE() extends BOOLEAN
case class FALSE() extends BOOLEAN

With sealed trait we can create limited set of possible values extending abstract data. Then we can easily define operations on those values and compiler will check if our functions are total (all possible values are handled) 

  object BooleanAlgebra {
        def negateTotalFunction(b: BOOLEAN): BOOLEAN = b match {
          case TRUE() => FALSE()
          case FALSE() => TRUE()
        }


        def negatePartialFunction(b:BOOLEAN):BOOLEAN=b match {
          case TRUE() => FALSE()   // warninng : not all cases handled
       }
      }

Exercises

Exercise : Level 1 - complete boolean algebra

  • implement all possible combinations of and and or operators

Exercise : Level 2 - matching on Try

  • In this exercise you need to convert list of string into list of ints.

Use prepared function : 

def parse(l: List[String]): List[Try[Int]] = l.map(s => Try(s.toInt))

Then map result of type List[Try[Int]] into List[Int]

  • In the second exercise from this section you need to calcualte size of an abstract list. List Data Type in scala has two values :: and Nil

Exercise : Level 3 - Abstract Numbers

Natural Number Data Type can be defined with only two values : Z(zero) and N(natural) (next number).

This data type can be then combined with different data type : Expression.

  • write evaulate function for both Data Types.

Exercise : Level 4 - Either[+A,+B]

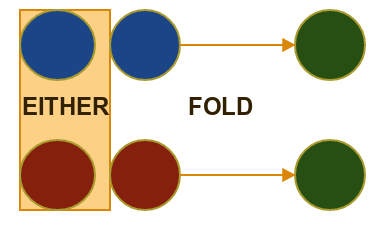
We can define a Data Type which holds an Union of two possible values : Either A (on left) or B (on right) .

Define method fold which apply one of two provided functions depending what value is in either : 

def fold[C](onError: A => C)(onSuccess: B => C)

Then test this Type in short example of web domain.

Decomposition

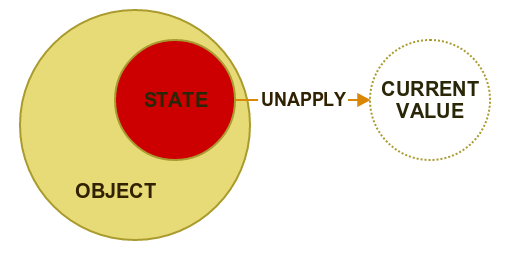
It is time to look under the cover of case class decomposition. In this section we are going to learn how relationship between a class and its compoanion object allow us to implement decomposition.

LAB FILE : https://github.com/PawelWlodarski/workshops/blob/master/src/main/scala/jug/lodz/workshops/fppatternmatching/exercises/PMPart4Decomposition.scala

In the demonstration part we can see an example of an unapply method which allow use of normal classes in pattern matching

class Wrapper3 private(val value: String)
object Wrapper3 {
        def apply(s: String) = new Wrapper3(s)
        def unapply(w3: Wrapper3): Option[String] = Some(w3.value)
}

Wrapper3("  --> example3 is working!") match {
        case Wrapper3(value) => println(value)
}

Encapsulation

This part also explains why pattern matching does not break encapsualtion. We have defined a class with some mutable state

class ObjectWithState() {
        private val history: ListBuffer[String] = ListBuffer()
        def act(message: String): Unit = history.prepend(message)
}

yet in unnaply we are not revealing internal representation of history

object ObjectWithState {
        def unapply(state: ObjectWithState): Option[(String, Int)] =
          state.history.headOption.map(lastMessage => (lastMessage, state.history.size))
}

neither it is revealed in pattern matching

val state = new ObjectWithState()
      state.act("message1")
      state.act("message2")
      state.act("message3")

state match {
      case ObjectWithState(lastMessage, allMessagesSize) =>
          println(s"  --> last message is : $lastMessage and there are $allMessagesSize messages")
}

Exercises

Exercise : Level 1 - write unapply

  • for a simpel class
  • for a Fraction which is represented as two integers (c,d)

Exercise : Level 2 - encapsulation of atomic state

  • implement thread safe method which increments value of global counter
  • implement unapply without revealing that inner representation is implemented as Atomic Integer
class Counter{
    private val state:AtomicInteger=new AtomicInteger()

    def increment:Int = ???   // increment counter in thread safe context
}

object Counter{
   def unapply(counter:Counter):Option[Int] = ???
}

Expression Problem

Now it's time for some reflection (not "code reflection" but "mind reflection"). Let's compare usage of ADT approach with other possible ways of modeling data in the context of so called Expression problem.

We will have set of Data Types representing Shapes and another set of possible operations. The purpose of this exercise will be to understand consequences of each approach.

Objects

  object ObjectLibrary {
      trait Shape {
        def area(): Double
      }
      class Circle(r: Int) extends Shape {
        override def area(): Double = Math.PI * r * r
      }
  }

We can model shape as object and use abstract methods to specify behaviour in each Data Type. 

import ObjectLibrary._
class Square(a: Int) extends Shape {
    override def area(): Double = a * a
}

val shapes: List[Shape] = List(new Circle(3), new Square(2))

println("* --> SHAPES AREAS")
shapes.map(_.area()).foreach(println)

Works well for new Types but shape interface is fixed and we can not add new operations. Because internal fields are hidden we CAN NOT also easily use those types in external operations.

Flat Data

We can just model Shape as a data records with public fields.

object DataLibrary {

   trait Shape

   case class Circle(r: Int) extends Shape

   def area(s: Shape): Double = s match {
      case Circle(r) => Math.PI * r * r
   }
}

Now it's easy to add new operations but we can not add new types without recompiling old operations

import DataLibrary._

def circumference(s: Shape): Double = s match {
    case Circle(r) => 2 * Math.PI * r
}

ADT

ADT nature give a rise of couple interesting concepts.

Look at the following code : 

object ADTLibrary {

sealed trait Shape {
   def area: Double = this match {
     case Circle(r) => Math.PI * r * r
     case Square(a) => a * a
   }
}
case class Circle(r: Int) extends Shape
case class Square(a: Int) extends Shape

}
  1. Because by definition we have limited amount of concrete types - and we know them all - so we can actually pattern match on them in abstract trait . This would a big code smell in OOP approach but here the trait is sealed so we are not going to add any new types and inhertiance polymorphism is not that crucial here.
  2. We decided to implement function inside data type but we could easily define behaviour outside data type if we want to design modules in a different way.
import ADTLibrary._

def circumference(s: Shape): Double = s match {
    case Circle(r) => 2 * Math.PI * r
    case Square(a) => 4 * a
}

Scala also allow us to add new functions into data with use of implicit conversions

implicit class ShapeUpgraded(s: Shape) {
     def implicitCircumference: Double = s match {
       case Circle(r) => 2 * Math.PI * r
       case Square(a) => 4 * a
     }
}

But what if I want to add new types? Then there are two options

  1. Or you knew that oryginally defined set of types is not complete and you should have model data with different approach
  2. You expected that values set is fixed and this expectations occured to be wrong. Well this is normal life - you need to review and refactor your design.

Exercises

Exercise : Level Boss - Right Biased Either**

Complete Right Biased Either definition

sealed trait RightBiasedEither[+A, +B] {
   def map[C](f: B => C): RightBiasedEither[A, C] = ???

   def flatMap[AA >: A, C](f: B => RightBiasedEither[AA, C]): RightBiasedEither[AA, C] = ???
}

case class RBLeft[A](a: A) extends RightBiasedEither[A, Nothing]
case class RBRight[B](b: B) extends RightBiasedEither[Nothing, B]

So you can write code like this : 

 val result1 = for {
     v1 <- RBRight(1)
     v2 <- RBRight(2)
     v3 <- RBRight(3)
 } yield v1 + v2 + v3

 val result2 = for {
     v1 <- RBRight(1)
     v2 <- RBLeft("There is an error")
     v3 <- RBRight(3)
 } yield v1 + v2 + v3

Bonus

As a bonus we are going to look at two small things :

  • @switch annotation
  • using external variables in pattern matching

We can annotate matched variable with @switch annotation

val input1=1
val result1=(input1: @switch) match {
    case 1 => "value is one"
    case _ => "value is not one"
}

And if compiler will not raise a warning then in bytecode we have relatively fast instruction tableswitch

In the following case a warning will be raised 

val input2=1
val result2=(input2: @switch) match {
      case 0=> "value is zero"
      case `input1` => "value is one"
      case _ =>   "value is something else"
}

We also see how to use external variable in pattern matching : case input1 => "value is one" . Instead of those funny qoutes we could also call this variable with capital letter and then by convention it's value would be used in PM but in my opinion this approach is very error prone.

Sources

results matching ""

    No results matching ""