Functions in Scala - Intro
We are going to learn :
- How to define functions in Scala with/without synthatic sugar. How to compose function and how to define and use popular datastructures in FP : Tuples.
- How using "Function as a value" help us achieve better modularisation in the code and reduce repetition
- Scala is a Hybrid Language which connects Functional Programming with Object Oriented Programming. We will see how we can use functions and object methods to create code which is easier to maintain. We will also see how function partial application can reduce coupling.
- How we can manipulate function structure to adapt already available structures to our needs. And how we can easily inject values/objects into functions to parameterize them almost like in Di framework
- What concepts like partial function and total function have to do with bugs and how Option and similar constructions allow us to use pure functions in the real world
- As a bonus we are going to experience pain of using mutable structures and see when this pain is necessary (but we have good pain killer called "encapsulation").

Part 1 : Define a Function
In Scala you can define a function in couple ways :
a) - anonymous class
val anonymousClassForm:Function[Int,Int]=new Function[Int,Int]{
override def apply(i: Int): Int = i+1
}
b) - anonymous class with type alias
val typeAlias: Int=>Int = new Function[Int,Int]{
override def apply(i: Int): Int = i+1
}
c) - one liner - lambda version
val shortWithType: Int=>Int = i=>i+1
and the shortest one
d)- underscore version
val f:Int=>Int=_+1
Composition
When you have couple functions you can easily combine them into single function:
val parse: String => Int = s=>s.toInt //exercise - make short with underscore
val square:Int=>Int = i=> i * i
val squareString=parse.andThen(square)
last line can be also written as :
val squareString=parse andThen square
because when you have a method with only one parameter you can omit dot and braces. You may ask "how function can have a method?" We will answer this question in module 3.
Tuples
Tuples are very useful structures because they are like "ultimate abstract DTO". You have n public fields of different types. Because of this structure generality you also have ready to use functions which operate on it.
What is important for now is that you declare a tuple in this very easy way :
val t3=("a",1,false)
Closure
In a function you can relate to a variables available in a context outside the function body. This may be useful for read only settings but may be dangerous if function result depends on mutable value.
val config=Map[String,Double]("tax"->0.23)
val gross=(net:Int)=>config("tax") * net + net
Exercises
Level 1
Define and compose simple functions
Level 2
Write custom andThen and compose (without using Function.andThen or Function.compose)

Level 3
- Write andThen with Generics (without using Function.andThen or Function.compose)
- As an introduction to the next topic - in method andThenSeq compose List of functions
Part 2 : Function as a value
How exactly treating function as a value can help us reduce code repetition?
Take a look at those two code fragments :
def sum(init:Int, es:Seq[Int]): Int ={
var result=init //var is bad but here it is encapsulated and fucntion is short
for(e <- es) result=result+e
result
}
def multiply(init:Int, es:Seq[Int]): Int ={
var result=init
for(e <- es) result=result*e //only one difference
result
}
They differ in only one tiny line
result*e or result+e
Normally in Object Oriented language we would try to parameterize this logic by extracting it to a parameter. But what would be a type of this parameter? Maybe SomeSpecificStrategy or something similar. But here we have to our disposal very general construct which can easily model this behavior - a function!
val add=(result:Int,element:Int) => result+element
val multiply=(result:Int,element:Int) => result*element
And we can define both of those operations in context of generic loop construction
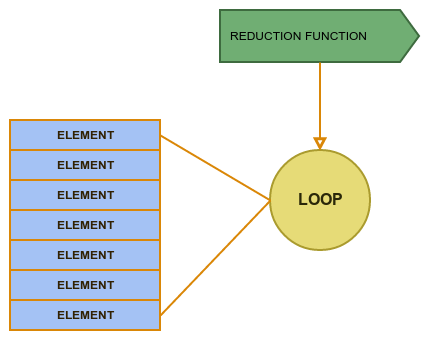
def reduce(init:Int,es:Seq[Int], op: (Int,Int)=>Int): Int ={
var result=init
for(e <- es) result=op(result,e) //only one difference
result
}
Generics
We will take closer look at this concept in the next section but we can build a more powerful abstraction with generics :
def reduceGeneric[A](es:Seq[A],init:A, op: (A,A)=>A): A ={
var result:A=init
for(e <- es) result=op(result,e) //only one difference
result
}
Now we are not limited to Integer Sequences.
a Function receiving a Function
Till now we considered methods receiving function. What signature would have a function receiving other function as an argument?
Normal Function looks like this
val f:A=>B = ....
'A' can be anything : Int,Double ,Boolean , String . So maybe 'A' can be an other function?
val f:(C=>D) => B = fcd=> fcd(???)
what could we pass to this function? Technically we don't have access to any value with type 'C' so maybe some general value from external context? We could also provide an additional parameter and we would receive curried function which will be described in the next section
val f:C=>(C=>D)=>B = c=>fcd => fcd(c)
This looks very abstract so some more concrete example may be useful.
val ints=Seq(1,2,3,4,5)
val mapReduceClosure: (Int=>Int) => Int = f=>ints.map(f).reduce(_+_)
Loan pattern
In general the loan pattern shows how to separate Resource lifecycle from business operation on this resource. This concept may be interesting because people like patterns :)
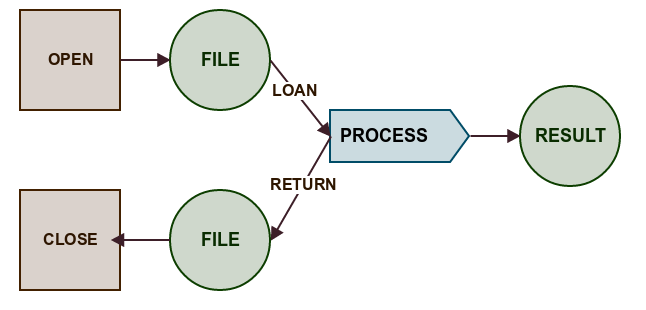
So we have a simple business function which is very easy to test
val countLines:Iterator[String] => Int = it=>it.size
And general structure responsible for resource management :
def loanFile[A](path:String,f:Iterator[String]=>A): A ={
val source = scala.io.Source.fromFile(path)
try{
f(source.getLines())
}finally{
source.close()
}
}
Exercises
Level 1
We are going to experience how treating a function as a value simplifies operations on collections
- implement high-order function map for specific types (applies function to each element)
- implement filter function for specific types
- practice defining complex function types
Level 2
- implement generic versions of map and filter
Part 3 : Functions and Methods
In later part we will focus on a differences between those two constructions to better understand in which situation use each of them but now let's focus on similarities.
First is that we can easily move between one form or the other. If a method receive one parameter we can convert it into a function which also receive one parameter of the same type.
def method(s: String) = {
s.toInt + 20
}
// you need to put underscore to signalize that you want to convert method and not to invoke it.
val f: (String) => Int = method _
Partial Application
From time to time you can spot strange method definition which has multiple pair of parenthesis
def calculateGross(tax: Double)(net: Int) = net + net * tax
This notation gives you two great things :
1) You can apply first argument independently from the second one so technically this works a little bit like dependency injection 2) If function uses generics and the first parameter is set then it may be not necessary to provide type for the second element.
def mapCurrying[A,B](s:Seq[A])(f:A=>B) = s.map(f)
//standard version :
mapCurrying(Seq(1,2,3))((i:Int)=>i+1)
//with detected type
mapCurrying(Seq(1,2,3))(i=>i+1)
//shortest version :
mapCurrying(Seq(1,2,3))(_+1)
When second argument is a function then we can use braces instead of parenthesis
mapCurrying(Seq(1,2,3)){i=>
i+1
}
This may be specially useful when we want to build 'custom language structures'
loanFile("/tmp/file.txt"){ lines=>
lines.foreach(println)
lines.size
}
Tail recursion
Tail recursion is a "recursion without stack explosion". When the last call has the same signature as a initial function then compiler may use the same stack cells for next invocation
@tailrec
def sumRange(start:Int,stop:Int,acc:Int=0): Int ={
if(start>stop) acc
else sumRange(start+1,stop,acc+start)
}
In scala we can use annotation @tailrec to make sure that our implementation correctly use tail recursion
Exercises
Level 1
- practice method <---> function conversion
Level 2
- Use curried method notation to build custom structures to perform safe operations
- Use tailRec
Level 3
- Write recursive versions of map and filter
Part 4 : Manipulating Function
Because we are treating functions as a value so not only can pass it or call it but also we can create a function on the fly as any value or modify it inside methods.
So for example if a want to have a factory method which returns a function then I would wrote this simple code :
def createIncrementFunction():Int=>Int = i=>i+1
val increment:Int=>Int = createIncrementFunction() //method invocation and funciton assignment
increment(1) // function invocation

To make code easier to read we can define special aliases for function types :
type Increment = Int=>Int
def createIncrementFunctionAlias():Increment = i=>i+1
Of course in a factory method we can inject some parameters into the function
type Currency = String
def injectCurrency(curr : Currency): Double => Currency = amount => amount+curr
val dollars: Double => String = injectCurrency("$")
dollars(12.73)
Decorate
If we can pass a value into method and inject this value into function then we can implement more powerful operations by passing a function into those methods.
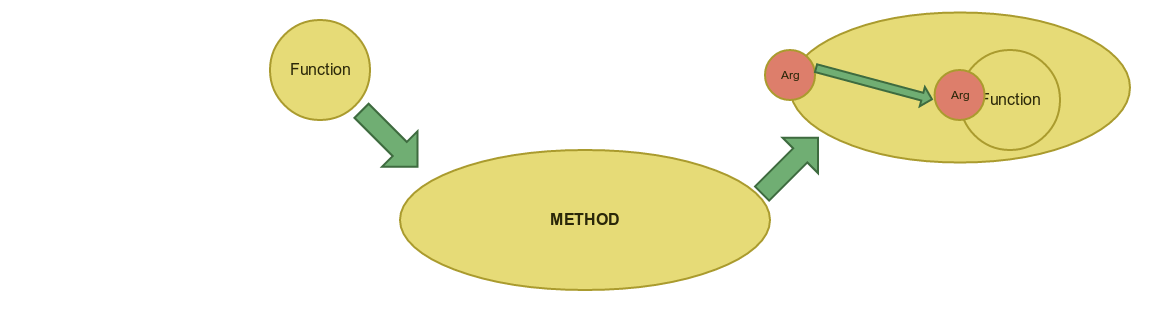
As a simple illustration of this process lets write a method which adds logging to any passed function :
def withLogging[A,B](f:A=>B) : A=>B = //A=>B - the same type
a=>{
println("INFO : invoking with arg : "+a)
f(a)
}
Manipulate Signature
The last example demonstrated adding new functionality to already defined function but we can even transform function itself and change its signature.
For example this is how we can implement "meta function" which partially apply first argument to a given function
def partial[A,B,C](f:(A,B)=>C,arg:A) : B=>C
But what if we want to partially apply second argument? Then we can combine this transformation with another meta-method which swaps arguments
def swap[A,B,C](f:(A,B)=>C):(B,A) =>C
Possibilities are limitless!
Domain example
At the bottom of the file you can find bigger example of using type aliases and currying to define small financial domain.
Exercises
Level 1
- create functions in methods
- inject parameters to functions created on the fly
- decorate function
Level 2
- implement curry and uncurry to manipulate function signature
Level 3
- use provided "domain library" to implement simple financial service with curied methods
Part 5 : Real World and Partial Functions
Till now we pretended that when you call a function with any argument than everything works fine. This is not always the case. For example when we are converting String to number the input parameter may not be a number at all.
So in this case a parse function is not a defined for every possible input and has a limited domain. We can call it a partial function and we can come with new bug definition that : bug occur when we are treating partial function as a total function
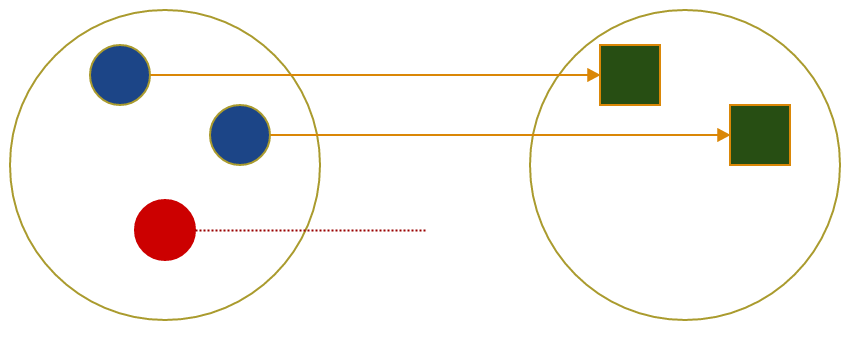
In scala there is a special type to represent partial function.
val partialDivide =new PartialFunction[(Int,Int),Int] {
override def isDefinedAt(tuple: (Int, Int)): Boolean = tuple._2 != 0
override def apply(v: (Int, Int)): Int = v._1/v._2
}
partialDivide.isDefinedAt(4,0) // false
Partial -> Total
There is another way we can handle this situation. We can convert partial function to total function by using special types to signalize partial function context.
One of those types is Option which symbolize potential lack of value
Following piece of code shows how to combine pure functions with option type to obtain pure functional operation in context of missing value.
val pureFunction:Int=>Int = i=>i+1
val parseTotal : String=>Option[Int] = s=>
try{
Option(s.toInt)
}catch{
case e:Exception => None
}
parseTotal("10").map(pureFunction) //Some(11)
parseTotal("aaa").map(pureFunction) // None
Exercises
EXERCISE FILE :
Level 1
- implement safe get on java.util.HashMap
Level 2
- write universal converter from partial function to total function
- decorate function with nullchecks and conversion to option
Level 4 - BOSS
/**
* .____ .__ _____ __________
* | | _______ __ ____ | | / | | \______ \ ____ ______ ______
* | | _/ __ \ \/ // __ \| | / | |_ | | _// _ \/ ___// ___/
* | |__\ ___/\ /\ ___/| |__ / ^ / | | ( <_> )___ \ \___ \
* |_______ \___ >\_/ \___ >____/ \____ | |______ /\____/____ >____ >
* \/ \/ |__| \/ \/ \/
* . ____ ____ ____________________
* /\|\/\ /\|\/\ /\|\/\ /\|\/\ | | | \_ _____/\__ ___/ /\|\/\ /\|\/\ /\|\/\ /\|\/\
* _) (__ _) (__ _) (__ _) (__ | | | || __) | | _) (__ _) (__ _) (__ _) (__
* \_ _/ \_ _/ \_ _/ \_ _/ | |___| || \ | | \_ _/ \_ _/ \_ _/ \_ _/
* ) \ ) \ ) \ ) \ |_______ \___|\___ / |____| ) \ ) \ ) \ ) \
* \/\|\/ \/\|\/ \/\|\/ \/\|\/ \/ \/ \/\|\/ \/\|\/ \/\|\/ \/\|\/
*/
- implement lift function which "lifts" any function into optional context
def lift[A,B](f:A=>B) : Option[A] => Option[B]
This is a very short function but for people who are moving from imperative world to more declarative approach implementation may be very cryptic and hard to understand at the beginning.
Bonus : Mutability - Good & Bad
When you see following statement :
1+1+2+1*1*1*2*2+2
and you are asked "what is the value of 1 after this operation?" Then response is obvious and question seems silly. But when you an object instance with an internal state and perform some set of operations
object.op(value1).op(value2).op(value3)
Then answer is not that obvious. To demonstrate it better let's build MutableNumber class.
// var - variable which can be changed
class MutableNumber(var value: Int) {
// <- mutate state
def +(other: MutableNumber) = {
this.value = this.value + other.value
this
}
def *(other: MutableNumber) = {
this.value = this.value * other.value
this
}
override def toString() = s"${value}"
}
This class has a state and each operation changes it's state so for example three.plus(two) changes state to five
val two=new MutableNumber(2)
val three=new MutableNumber(3)
val normalResult=(2+3)*2+2 //easy to analyze
val mutableResult=(two + three)* two + two //???
Can you guess the result? Well it is:
50 !
If this seems strange than this exactly what is happening when you are working with mutable state. Each operation changes object behavior. To understand one operation you need to know the full history!
But it may be faster
If observer is not aware that you are using mutable structure then it is well encapsualted and should not trigger new bugs.
def filter[A](s:List[A])(p:A=>Boolean): List[A] ={
val result=new ListBuffer[A]()
for(e <- s) if(p(e)) result += e
result.toList
}
In example above we are using mutable ListBuffer but because it is used only locally inside function reader can use filter without any awareness that there is mutable structure beneath it!
filter(List(1,2,3,4,5))(i=>i>3)