Functional Programming in the Real World - Handling Effects
During those workshops we are going to learn how to handle situation when need to handle side effects and create functions which may return unpredictable results.
Plan
- Understand what kind of problems may rise when effects are hidden and not explicitly sygnalized in the type system..
- Learn how make an Effects part of Type system
- How to compose mulitple effects of the same type
- How to represent effects of Optionality , Failure , Time and Non Determinism.
- How to use pure functions in the context of side effects
Part 1 - functions in the real world
First we are going to provide couple implementations of a function which return first element of a list
def firstElement1Exception(l: List[Int]): Int = l.head
def firstElement1Null(l: List[Int]): Int = if (l.size > 0) l.head else null.asInstanceOf[Int]
def firstElement1OrDefault(l: List[Int], default: Int): Int = if (l.size > 0) l.head else default
def firstOptionalElement(l: List[Int]): Option[Int] = if (l.size > 0) Some(l.head) else None
The problem is that an empty list does not have the first element - how we can handle this situation?
In the demonstration part we are going to check how to safely use each variant of these function and as a consequence - what construction will appear in our code.
- In try example we need to add try-catch block. We "need" but we are not "forced"to add it. So there is always danger that we will not handle it properly. Later we will discuss why checked exception did not solved this problem
- We could return null but does caller know that we could return null?
- We could provide default value. But do we always have logical default value. What if we need to distinguis between natural and default result?
- Finally we can make this edge case a aprt of Type system
Exercises
In the exercises section we are going to execute one of the two following scenarios :
- call UsersDAO and find given User
- convert user into HTML
- display his info on a sucess page
or in case of missing user in database
- call UsersDAO but there is no user with given Id
- display error page
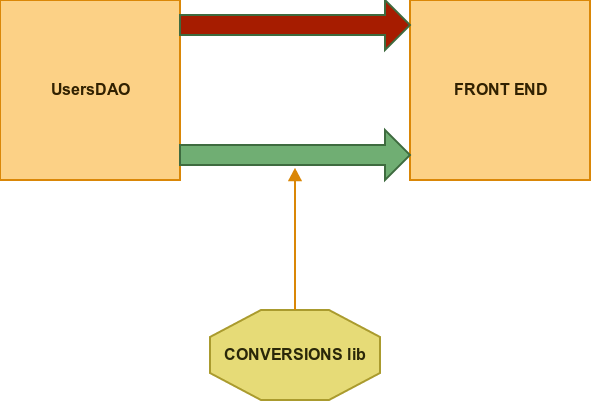
Exercise : handle both scenario with possible missing value
In dao you can find 4 variants of find emthods :
def findOrNull(id: Int): User = if (database.contains(id)) database(id) else null
@throws(classOf[Exception])
def findOrException(id: Int): User = if (database.contains(id)) database(id) else throw new RuntimeException("break computation!")
def findOrDefault(id: Int, defaultUser: User): User = if (database.contains(id)) database(id) else defaultUser
//what is default here?
def findOption(id: Int): Option[User] = database.get(id)
Try to handle two mentioned business scenarios with each variant and check what consequences each solution triggers.
There is provided skeleton for each part in the code
//PART1 - OPTION
// val optionalUser = UsersDAO.findOption(1)
// displayPage(userToHTML(optionalUser.get))
// displayError("There is no user with this id")
Part 2 - Understand Optionality Effect
In the last exercise we used Option just to sygnalize that value is potentially missing and then we really treated it like object representation of if condition which is actually a bad practice
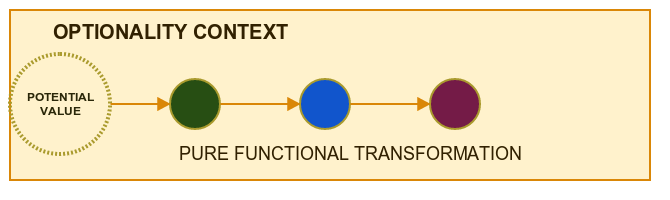
Having Option as a type allow us to execute pure functions which are referentially transparent in context of missing value
val some: Option[Int] = Some(7)
val multiplyByTwo: Int => Int = i => i * 2 //is this function pure ?
val display: Int => String = i => s" -- RESULT : $i" // does this function have any knowledge about context?
some.map(multiplyByTwo).foreach(i => println(s" -- multiplied by two : $i"))
some.map(multiplyByTwo).map(display).foreach(println)
But what if the value is really missing - what will be executed and how to handle this situation?
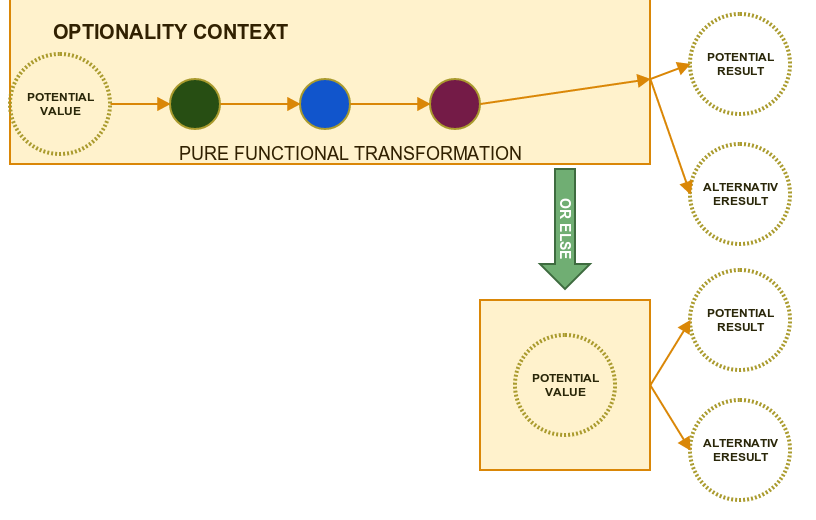
Because Option type has available set of very useful high order functions so it is very easy to use pure functions to handle happy path and also to build second path in case of empty value
val default = some.filter(_ > 10).getOrElse(-1)
some.filter(_ > 10).orElse(Some(-1)).map(i => s" -- filter(remove) & orElse -1 : i=$i").foreach(println)
some.filter(_ < 10).orElse(Some(-1)).map(i => s" -- filter & orElse : i=$i").foreach(println)
We can also use Pattern Matching to handle each Option type accordingly :
some match {
case Some(value) => println(s" -- pattern matching value : $value")
case None => println(s" -- pattern matching is empty")
}
finally we can just pass to option set of recipies in case of success and failure.
val onSuccess: Int => String = i => s"business value $i"
val onError: String = "raise an error"
val result = some.fold(onError)(onSuccess)
This is a lot of new knowledge - let's train it now
Exercises
Exercise : handle both scenario with high order functions
In following lines use combinators map and fold and also pure functions from Conversions and FrontEnd to implement both scenarios
val html1 = UsersDAO.find(1) //use map & fold
val html2 = UsersDAO.find(2) //use map & fold
In the following example try to use combinators map and orElse and getOrElse
UsersDAO.find(2) //use map & orElse & foreach to display result
val html3 = UsersDAO.find(2) //use map & getOrElse
Additional Exercise : implement lift function
As a warmup implement lift function which lifts pure functions into effects level
def lift[A, B](f: A => B): Option[A] => Option[B] = ???
Additional Exercise : implementing optionality with custom types
Now we have a custom type which symbolizes optionality
sealed trait Maybe[+A]
case class Just[A](value: A) extends Maybe[A]
case object Empty extends Maybe[Nothing]
implement lift and map fot this new type
def map[A, B](m: Maybe[A])(f: A => B): Maybe[B] = ???
def liftMaybe[A, B](f: A => B): Maybe[A] => Maybe[B] = ???
Part 3 - Multiple Optional Effects
Till now we analyzed only couple simple examples when we have a single Optionality Effect but what to do when we have multiple such types in our calculations?
For example we have a User who may or not have Page which may or not have Picture
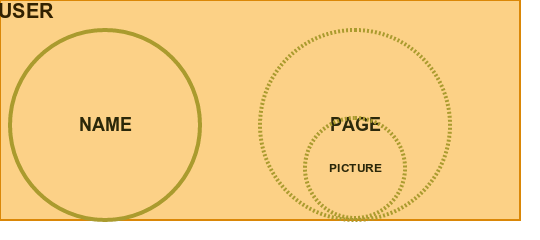
Take a look at the Exercise source code : https://github.com/PawelWlodarski/workshops/blob/master/src/main/scala/jug/lodz/workshops/fpeffects/exercises/EffectsPart3MultipleOptions.scala
In Demonstration you will find an example how to use the new operator flatMap . Each time when you have an effect and you want to perform transformation which also triggers the Effect - think flatMap
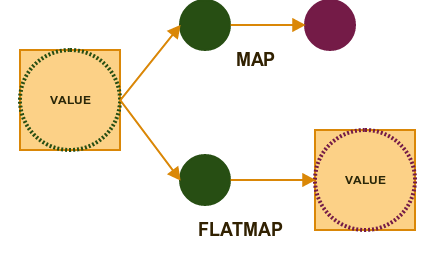
Exercises
Exercise : display User last meetup
find user last meetup and implement pure function which maps user to HTML
def userLastMeetup(id: Int): HTML = ???
def meetupHistoryToHTML(mh: MeetupHistory) = ???
In Our domain you have a meetup history record with optional picture
val meetupHistory1 = MeetupHistory("FP Scala", Some(Picture("SCALA_LOGO")))
val meetupHistory2 = MeetupHistory("FP Java", None)
The problem is that potenatial user maybe has just registered and he has no meetup history
val user1 = User(1, "FirstUser", "[email protected]", List(meetupHistory1, meetupHistory2))
val user2 = User(2, "SecondUser", "[email protected]", List())
Additional Exercise : implement flatMap for our custom type
def flatMap[A, B](m: Maybe[A])(f: A => Maybe[B]): Maybe[B] = ???
Additional Exercise : implement new combinator 'map2'
What if you have two Options and a two arguments pure function? We need to introduce a new operator which lifts multi-argument functions to effects level.
def map2[A, B, C](m1: Maybe[A], m2: Maybe[B])(f: (A, B) => C): Maybe[C] = ???
This is a prelude to a new very powerful Functional Programming Abstraction - stay tuned!

Part 4 - For Comprehension
When we have a lot of effect types using map and flatMap can make our code less readable.
val some1 = Some(1)
val some2 = Some(2)
val some3 = Some(3)
val some4 = Some(4)
val result = some1.flatMap { a =>
some2.flatMap { b =>
some3.flatMap { c =>
some4.map { d => a + b + c + d }
}
}
}
Fortunatelly Scala introduces a very powerful language construct - for-comprehension
val resultComprehension = for {
s1 <- some1
s2 <- some2
s3 <- some3
s4 <- some4
} yield s1 + s2 + s3 + s4
The result of both code samples is the same but the second one is a lot cleaner. During exercises we will gain some experience with usage of this construct.
Exercises
Additional Exercise : join optional values
Join couple optional values with for comprehension
def join(o1: Option[String], o2: Option[String], o3: Option[String]): Option[String] = ???
Additional Exercise : implement map2 for Maybe type
def map2[A, B, C](m1: Maybe[A], m2: Maybe[B])(f: (A, B) => C): Maybe[C] = ???
Additional Exercise : sequence of effects
//use foldRight & map2 || flatMap & map & recursion
def sequence[A](l: List[Maybe[A]]): Maybe[List[A]] = ???

Part 5 - Error Effect
While Option tell us that something Is present/Is missing Try is prepared to handle multiple error path for different exceptions
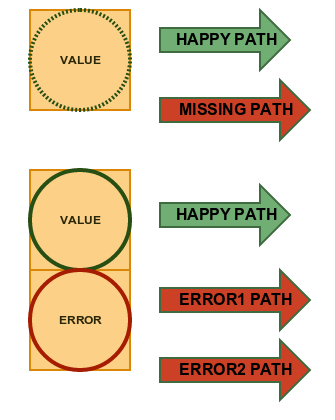
Try has two subtypes Success and Failure
println(s"\n -- pattern matching")
goodResult match {
case Success(lines) => println(s"file size PM : "+lines.size)
case Failure(exception) => throw exception
}
You can recover to happy path if you know how to handle specific exception
println(" \n -- Recover Bad")
badResult.recover{
case e:Exception => List(s"something went wrong : [${e.getMessage}]")
}.get.foreach(println)
or you can apply independent handler procedures
println(s"\n -- transform Good")
val businessFunction:List[String] => Try[Int] = l=> Try(l.length)
val errorHandler : Throwable => Try[Int] = _ => Try(0)
goodResult.transform(businessFunction,errorHandler).map(i=>s"file length $i").foreach(println)
Exercises
Exercise : add error effects
For comprehension may be useful here :
def tryToAdd(s1: String, s2: String, s3: String, s4: String) :Try[String] = ???
Additional Exercise : implement map2 and sequence for Try
def map2[A,B,C](t1:Try[A],t2:Try[B])(f:(A,B)=>C):Try[C] = ???
def sequence[A](l: List[Try[A]]): Try[List[A]]
Additional Exercise : implement map3 for Maybe type
A pattern starts to emerge
def map3[A, B, C,D](m1: Maybe[A], m2: Maybe[B],m3:Maybe[C])(f: (A, B,C) => D): Maybe[D] = ???
Part 6 - Some Theory - Effects and composition
But why exactly effects removed from type system cause so much problem? Let's imagine couple simple functions which we want to compose :
val toInt:String=>Int = _.toInt
val addOne:Int=>Int=_+1
val multiplyByTwo:Int => Int=_*2
val simpleComposition=toInt andThen addOne andThen multiplyByTwo
println(" -- pure result : "+simpleComposition("5"))
Everything works fine but there is something very dangerous lurking inside :
simpleComposition("notANumber") // this will throw an exception
Now look at this. Because Our function has hidden side effect it can return different result in different places of a program so Referential Transparency is broken as a start and we need to be prepared for all exceptions thrown by each function which composed the final one.
val resultWithSideEffect=try{
try{
simpleComposition("notANumber") //here returns -1
}catch {
case e:Exception => -1
}
// simpleComposition("notANumber") // here returns 0
}catch{
case e:Exception=> 0
}
// simpleComposition("notANumber") //here dies
Now what if we want to handle this situation and still keep simple types? Well we can not compose function which throws exceptions because it just leave computations so we must somehow signalize that actually our function has two possible paths :
val toIntWithException:String=>(Int,Exception)
But in case of happy path we don't have Exception and in case of exception we may not have value - we can use null to signalize this optionality - we already saw what kind of problems null generates.
val toIntWithException:String=>(Int,Exception)=input=>try{
(input.toInt,null)
} catch{
case e:Exception => (null.asInstanceOf[Int],e)
}
But what If second function has just simple type Int => Int ? We need need somehow to wrap this function into (Int,Exception) => Int ... ant then again we may encounter the same pronblem which solve set of embedded ifs
The truth is that function val toInt:String=>Int = _.toInt is a partial function To make it total we need to introduce Effects into Type system
val toIntTotal:String=>Try[Int] =input => Try(input.toInt)
now we can transform/map this value without looking for any hidden execution paths. In case of pure functions we have map combinator and we saw that we can easily mixIn other functions with effects with flatMap
Part 7 - Other Effects
Time
To symbolize Time Effect - calculations may be finished soon or never - Scala sues Future
For example we can have two external services and we need to wait untill information will move through wires.
object Service1{
def call(input:Int):Future[Int]=Future{
TimeUnit.MILLISECONDS.sleep(500)
input+1
}
}
object Service2{
def call(input:Int):Future[Int]=Future{
TimeUnit.MILLISECONDS.sleep(500)
input+2
}
}
Than we can build result with already known for comp[rehension
val comprehensionResult=for{
r1<-Service1.call(1)
r2<-Service2.call(r1)
} yield r2
comprehensionResult.onSuccess{
case v => println(s" -- comprehensionResult : $v")
}
Non Determinism
This may be surprise but effect of non determinism is a ... List of multiple values. Why?
Theoretically function can return only one value
y=f(x)
What if we have
f(x)=y1,y2...yn
How to specify what exactly is a result? For example we want to calculate root of a positive value
val allRoots:Double=>List[Double]=input => {
val result = Math.sqrt(input)
List(-result, result)
}
Now we can use high order functions to specify one final result
println("-- handling non determinism1 : "+allRoots(4.0).map(Math.abs).head )
println("-- handling non determinism2 : "+allRoots(4.0).filter(_>0).head )
We can also use special reduction oeprators
Let say we want to count profit made on a given day. We call for a purchase from that day and we receive multiple purchases.
val purchasesOnDate: String => List[Purchase]= _ match {
case ("01-01-2016") => List(Purchase("tv","01-01-2016",300),Purchase("console","01-01-2016",200))
}
Now we need to reduce our purchases to single value
println(" -- counting profit - moving from set of possible values into a single value")
val singleProfit=purchasesOnDate("01-01-2016").map(_.profit).reduce(_+_)
println(" -- singleProfit : "+singleProfit)
Exercises
Exercise : all possible combinations
You have two multi value results
val drivers=List(Driver("John"),Driver("Jane"),Driver("Kubica"))
val cars = List(Car("Polonez"),Car("Porsche"))
calculate possible combinations
def combinations():List[(String,String)] = ???
Additional Exercise : applying function with effects
map2 allow us to specify new very powerful combinator. Because map2 apply two-arg function to effects than we can close a Function (which is also a value in FP) inside an Effect and then we can apply this function multiple times in context of this effect.
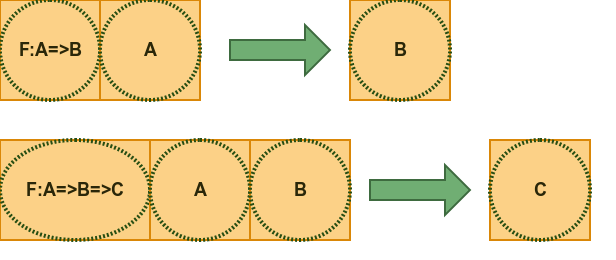
This may be more clear in code :
take look at function type: (Option[Int=>Int]) => (Option[Int] => Option[Int])
val applicative1ArgInt: (Option[Int=>Int]) => (Option[Int] => Option[Int]) =
function => firstOption => map2(function,firstOption)((f,argument)=>f(argument))
and the second one , again notice
(Option[Int=>Int=>Int]) => (Option[Int] => Option[Int=>Int])
val applicative2ArgIntInt: (Option[Int=>Int=>Int]) => (Option[Int] => Option[Int=>Int]) = function => firstOption =>
map2(function,firstOption)((f,argument)=>f(argument))
To see how universal this pattern may be try to implement map & map2 with it
def mapApp(o1:Option[Int])(f:Int=>Int):Option[Int] = ???
def map2App(o1:Option[Int],o2:Option[Int])(f:(Int,Int)=>Int):Option[Int] = ???
ADDITIONAL HARDCORE : universal mapN with APPLICATIVE FUNCTOR
If we want to generalize function from previous exercise it would look like this :
def applicative[A,B](fab:Option[A=>B])(oa:Option[A]):Option[B] = map2(fab,oa)((f,arg)=>f(arg))
Still it only handles Option type. We already had similar issue when we generalized map function during workshop 2.
We also saw that with map2 we can apply function in context of given effect. If we combine this with currying we receive a powerful abstract concept of applaying multiple arguments in context of a given effect
- Functor : (A=>B) => (F[A] => F[B])
- Applicative Functor : F[A=>B] => (F[A]=>F[B])
- Applicative Functor : F[A=>B=>C] => (F[A]=>F[B=>C])
- Applicative Functor : F[A=>B=>C=>D] => (F[A]=>F[B=>C=>D])
Cats library already provides Applicative Functors for most Effects. In cats they are called Apply
So Implement universal map2 and map3 with this pattern
def universalMap2[A,B,C,M[_]](m1:M[A],m2:M[B])(fab:(A,B)=>C)(implicit applicative:Apply[M]): M[C] = ???
def universalMap3[A,B,C,D,M[_]](m1:M[A],m2:M[B],m3:M[C])(fabc:(A,B,C)=>D)(implicit applicative:Apply[M]): M[D] = ???
Part 8 - Combine different effects
This is quite complex topic but I decided to put it here just for completness of Effects topic
What if for example we have two effects at the same time? Foe example when we are calling external webservice we have time - Future[T] and posibility that given value will be missing - Option
In this situation we can use predefined MonadTransformer . In Graphical explanation it will look like this :
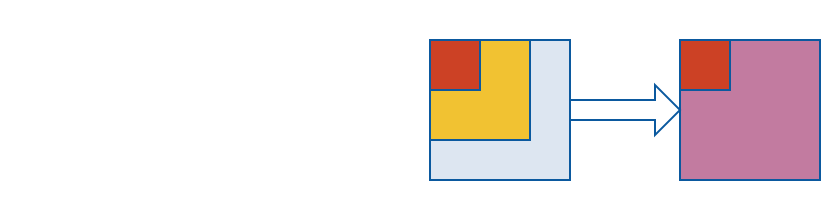
Let's imagine that in the code we have two web services :
def service1(name:String) : Future[Option[Int]] ...
def service2(id:Int) : Future[Option[Company]]
We can not write simple for comprehension because argument of second web service Int is not the same as result of the first one Option[Int].
Solution with MonadTransformer
import cats.data.OptionT
import cats.std.future._
val result=for{
id<-OptionT(service1("company1"))
company<-OptionT(service2(id))
} yield company.info
val finalValue: Future[Option[String]] = result.value