Functional Programming in Scala workshop1

Motivation

The main purpose of this workshop is to learn Functional Paradigm as a "general Idea". So skills learnt during these exercises will be potentialy useful in any programming language with functions as so called "first class citizens".

We chose Scala for this workshop because it is more "FP friendly" than Java and also scala seems to be natural bridge from OOP to FP for Java developers. So along with learning FP we will learn some scala syntax to better udnerstand some mechanisms which were (or still are) not available in Java.

Inspiration

https://www.manning.com/books/functional-programming-in-scala

Plan

  1. Short Practical Exanmple - we are going to analyze practical short example to understand the potential of FP.
    1. In this example we will learn what is Property Based Testing and see it's power when we are testing stateless functions
  2. Set of short Exercises where we will learn about:
    1. "Function mechanics" to better understand how syntatic sugar can help us and what is Function made of in scala.
    2. After understanding mechanics we will research Function nature - especially we will check why in FP Function is called "first class citizen".
  3. Then we are going to take a look at some FP theory - this time what is referential transparency and why it is so important.
  4. Decompilation Lab - Becauswe practical FP needs to connect mathematical abstraction with "practical runtime environment" so here we will also do some exercises with decompilation to not lose connection with the real world
  5. Homework - 2h workshop is just a begining - you need to practice!

Practical short example

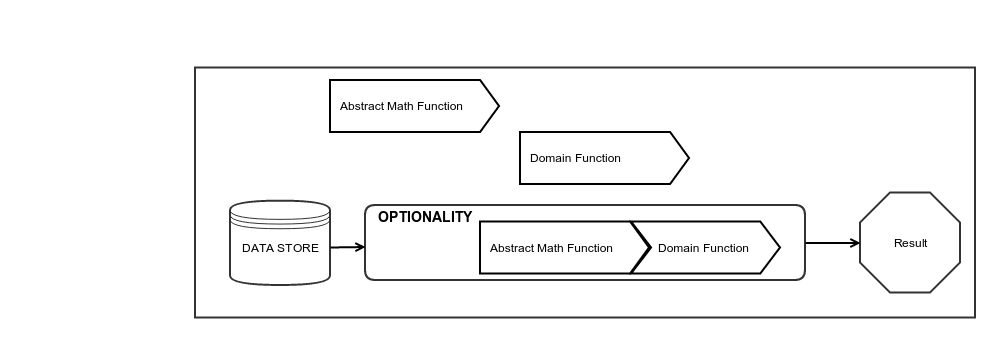
The source code of this example may be found here : https://github.com/PawelWlodarski/workshops/blob/master/src/main/scala/jug/lodz/workshops/fp1/exercises/ScalaFp1PracticalExample.scala

Domain and value classes

The following example simulates situation when there is a system with some products and those products are aggregated in a specific purchase.


//Our custom domain lib
  object DomainLib{
    case class Product(name:String,price: BigDecimal)
    case class Purchase(id:Int,purchasedProducts:List[Product])
  }

//Database emulation
  private val products:Map[String,Product]=Map(
    "tv"->Product("tv",BigDecimal("3000")),
    "keyboard"->Product("keyboard",BigDecimal("120")),
    "mouse"->Product("mouse",BigDecimal("70")),
    "headphones"->Product("head phones",BigDecimal("200"))

  )

  private val database:Map[Int,Purchase] =Map(
      1 -> Purchase(1,List(products("tv"),products("headphones"))),
      2 -> Purchase(2,List(products("keyboard"),products("headphones"),products("mouse")))
  )

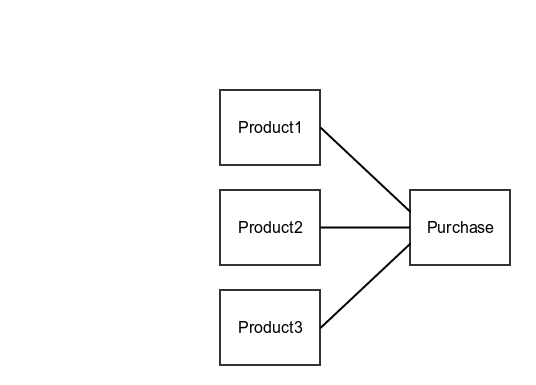
Here we are assuming that not all students may be accustomed with scala syntax so a very short introuduction may be needed.

There may be a question about case class. Again let's simply assume it is just a class with generated getters. More info -> http://docs.scala-lang.org/tutorials/tour/case-classes.html

Lab

In the first exercises we need (together) to implement 3 missing functions.

  • findPurchase of type Option[Purchase] - this method returns data from database. Return is optional because given Id may exist in database or not
  • domainFunction of type Purchase => Seq[BigDecimal] or Function[Purchase,Seq[BigDecimal]]
  • some generic math function of type Seq[BigDecimal]=>BigDecimal or Function[Seq[BigDecimal],BigDecimal]

??? is just a placeholder so that code without methods could compile.

//lab 1
def findPurchase(id:PurchaseId):Option[Purchase] = ???

//lab 2
val domainFunction: Purchase => Seq[BigDecimal] = ???

//lab 3
object MathLib {
  val genericMathFunction:Seq[BigDecimal]=>BigDecimal = ???
}

And after it is completed there is a small demonstration of how it is easy to compose independent functions into final operation

In the code below we are composing two functions from two different worlds. One is our domain function which is avare of Purchase concept and the second one is a very generic mathematical function from an external library

  def main(args: Array[String]) {
    //Composition of two completely independent pure function
    val pureDomainFunction: (Purchase) => BigDecimal =domainFunction andThen genericMathFunction

Then we can move to another interesting thing - Effects. In this workshop we will limit our exposition to effects only to Optionality to not confuse participants.

So our exercise function return an optional value : 

def findPurchase(id:PurchaseId):Option[Purchase] = ???

Because we are operating on Option[T] we can easily use our pure domain function in the context of a value which Maybe exists (but maybe not)

Property Based Testing

There is a separate workshop about Property Based Testing and you can find materials here --> https://pawelwlodarski.gitbooks.io/workshops/content/scalacheck.html

In our exercise we can use PBT to check both of our functions : generic and domain one.

 property("Math generic function should sum all decimals"){
    forAll(bigDecimalList){ (bs: List[BigDecimal]) =>
        MathLib.genericMathFunction(bs) shouldBe bs.sum
    }
  }


  property("domain function will extract all prices"){
    forAll(purchaseGen){ (purchase: Purchase) =>
      ScalaFp1PracticalExample.domainFunction(purchase) shouldBe purchase.purchasedProducts.map(_.price)
    }
  }

In this exercise the most important thing to learn is a fact that there is something like Property Based Testing and that everyone (when using stateless functions) can use it. Here we have two properties - checking sum for generic math function and checking that prices extraction awlays works.

As part of exercises we can print out arguments generated to checks but still the main educational value is to learn that something like PBT exists and you can use it when you are testing pure functions.

Above the checks participants can see how some generators are created - for this exercises details can be ignored.

Exercises

How function is implemented

Let's start with a function form which seems to be the most natural :

val addOneToX: Int=>Int = x => x+1
  • It is a Value
  • It hase a type which describes relation between input and output
    • Int=>Int - input is Int and output is Int
  • It has a body x=>x+1 which describes what happens with input

The second form is shorter but may be less readable if you don't have enough experience with scala syntax

val addOneToXShort:Int=>Int = _+1
  • the main difference is in the body. In original form it was x=>x+1 so if I don't want to repeat argument name I can just use unnamed placeholder. So the syntax _+1 mean "add one to first argument"

And To gain better understanding of how function is implemented let's remove all syntatic sugar

val addOntToXFull:Function[Int,Int]=new Function[Int,Int]{
    override def apply(v1: Int): Int = v1+1
  }

This is very cumbersome OOP interpretation of a function

  • Instead of type alias Int=>Int we have interface name Function[Int,Int]
  • Instead of functional representation of a computation x=>x+1 we have a method implementation

Exercise : implement all function forms for a function multiplyXByTwo*

lazy val multiplyXByTwo: Int=>Int = ???
lazy val multiplyXByTwoNoAlias: Function[Int,Int] = ???
lazy val multiplyXByTwoFull:Function[Int,Int] = ???
lazy val multiplyXByTwoShort:Int=>Int = ???

As an additional exercise you can do the same thing for a function addTwoNumbers

Use prepared property based tests :

https://github.com/PawelWlodarski/workshops/blob/master/src/test/scala/jug/lodz/workshops/fp1/exercises/ScalaFP1ExercisesFunctionImplementationCheck.scala

and boolean checks in function main

Exercise - Function as a value

Now we are going to do soem short exercises which will show concept of a "function as a value"

Exercise code:

https://github.com/PawelWlodarski/workshops/blob/master/src/main/scala/jug/lodz/workshops/fp1/exercises/ScalaFP1FunctionAsAValue.scala

Practice : pass function to method

First take a look at the following code. In the first line you can see that we declared a function and then we have a different construct which method with two parameters. 

 val fun:Int=>Int = x=>x+1

  def logInvocation(f: Int=>Int, arg:Int):Int={
    val result=f(arg)
    println(s"invoking function with arg : $arg and result is : $result")
    result
  }

In the method declaration the first argument is a function istelf and the second one is a value which we are going to pass to a function.

Main thing to learn: a Function which is passed as an argument is invoked in method body - not earlier!

Exercise : pass function to a method

Function specifications for all exercises are in the main method

Implement method which will parse string argument before passing it to a function with Integer argument

def invokeParsed(f:Int=>Int,arg:String):Int= ???
//check 
invokeParsed(fun,"5")==6

ADDITIONAL EXERCISE

Implement functions with 0 arguments which will return a String. Second parameter n tells how many times result of invocation should be add to result list.

def generateN(f:()=>String,n:Int) : List[String] = ???
//check
generateN(()=>"FP",2)==List("FP","FP")

Practice : Return a function from a method

Look at this : 

def createSomeFunction():Int=>Int = x=>x+5
println("create some function : "+createSomeFunction()(1))

There are two pairs of parenthesis. First one is method invocation ande the second one is function invocation

Exercise : return function from a method

Create at least one of following methods

def createHello() : String => String = ???
//check createHello()("Romek") == "Hello Romek"
def createNegation() : Int => Int = ???
// check createNegation()(10) == -10
def createAddTwoNumbers() : (Int,Int) => Int = ???
//check createAddTwoNumbers()(1,3)==4

Exercise : change a function

def parseArgumentBeforeCallingFunction(f:Int=>Int) : String=>Int = ???
//check parseArgumentBeforeCallingFunction(fun)("3")==4

def addLoggingToAFunction(f:Int=>Int) : Int=>(Int,String) = ???
//check addLoggingToAFunction(fun)(1)==(2,"arg=1")

Functions and methods

And finaly let's take a look at the last example - you can pass w method where a function is expected - this is Scala's hybrid nature.

def addToOneMethod(x:Int)=x+1
logInvocation(addToOneMethod,1)

And let's take a look how to translate from a method to a function. (Additional explanation during workshops if necessary)

val functionFromMethod: (Int) => Int = addToOneMethod _

Practice : Compose functions

Source code for the exercises : https://github.com/PawelWlodarski/workshops/blob/master/src/main/scala/jug/lodz/workshops/fp1/exercises/ScalaFP1ComposeFunctions.scala

There are two main build in functions responsible for function composition

  • andThen - it composes functions into natural flow for readers f1->f2->f3
  • compose - it composes functions into "mathematical flow" f3<-f2<-f1 or f3(f2(f1(x))
//Analogy
ps -ax|grep java  (f andThen g)
f(g(x))  (f compose g)

In code it looks like this :

val parse : String => Int = s=>s.toInt
val neighbours:Int=>List[Int] = x=>List(x-1,x+1)

parse.andThen(neighbours)("3") == List(2,4)
neighbours.compose(parse)("5") == List(4,6)

Exercise : implement andThen and compose by yourself

//  customAndThen(f1:Function[String,Int], f2:Function[Int,List[Int]]):Function[String,List[Int]]
def customAndThen(f1:String=>Int, f2:Int=>List[Int]):String=>List[Int] = ???
def customCompose(f1:Int=>List[Int], f2:String=>Int):String=>List[Int] = ???

Remember that this type at the end String=>List[Int] means that you need to return a function.

ADDITIONAL

implement generic version

 def customAndThenGeneric[A,B,C](f1:A=>B, f2:B=>C):A=>C = ???
 def customComposeGeneric[A,B,C](f1:B=>C, f2:A=>B):A=>C = ???

implement sequence of functions reduction with andthen

def andThenSeq(fs:Seq[Int=>Int]): Int=>Int = ???
//check andThenSeq(Seq(x=>x+1,x=>x*2,x=>x+5))(1)==9

Theory - Referential Transparency

Time for some theory decorated with a practical exercise where participants finally will be able to write Property Based Test on their own.

What is Referential transparency?

Two quotes borrowed from this book : https://www.manning.com/books/type-driven-development-with-idris

(Why Im quoting Idris book in the middle of FP in scala workshop - because I had this book opened on pure functions chapter when I was writing this part - for sure in FP in Scala we can find similarly good quotes but I thought that by mentioning Idris which is totaly exotic for most people we will see how FP concept is universal)

quote1: "An expression (e.g. a function call) in a function is referentially transparent if it can be replaced with its result without changing the behaviour of the function."

quote2 "because if a function has no side effects is defined entirely by its inputs and outputs"

Check the code : https://github.com/PawelWlodarski/workshops/blob/master/src/main/scala/jug/lodz/workshops/fp1/exercises/ScalaFP1ReferentialTransparency.scala

You will see two functions one called pure and the second one inpure. During workshops we are going to discuss what are the consequences of inpurity.

var globalState:Int=0

  val pure:Int=>Int= x=>x+1
  val impure: Int=>Int = x=>{
    globalState=globalState+1
    x+1+globalState
  }

Exercise : implement property based test to check if function is pure

Exercise code :

https://github.com/PawelWlodarski/workshops/blob/master/src/test/scala/jug/lodz/workshops/fp1/exercises/ScalaFP1ReferentialTransparencyCheck.scala

Hint - Just try to simulate N call of a given function and check if N generated values fullfill RT rule.

Buffer exercises

If there will be some time left during workshops then we can do those exercises. Otherwise we will move them to workshop 2.

source : https://github.com/PawelWlodarski/workshops/blob/master/src/main/scala/jug/lodz/workshops/fp1/exercises/ScalaFP1BufferExercises.scala

Exercise : implement partial application

Look at return parameters - you need to somehow remove first argument

val calculateTax:(Double,Int) => Double = (a,b)=>a*b
val calculateVat : Int=>Double = calculateTax(0.23,_:Int)

def partialApplication(f:(Double,Int)=>Double, firstArg:Double): Int=>Double = ???

Exercise : implement currying

In the production world currying is the easiest way to inject dependency

//CURRYING
lazy val curriedTax : Double=>Int=>Double= tax => sum=>tax*sum
lazy val curriedJoinString3 : String=>String=>String=>String = s1=>s2=>s3=>s1+s2+s3

This may be not intuitive at the begining. Int=>Int=>Int can be also written as Int => (Int => Int) - so one Int argument and a function as a result

//first try just to create curried functions
val curriedAdd2: Int=>Int=>Int= ???
val curriedAdd3: Int=>Int=>Int=>Int= ???
val curriedAdd4: Int=>Int=>Int=>Int=>Int= ???

//and now implement high order functions which change multiarguemtn function into curried one
 def curry[A,B,C](f:(A,B)=>C):A=>B=>C= ???

Exercise : implement uncurrying

This is an opposite operation to the previous one

def uncurry[A,B,C](f: A=>B=>C) : (A,B)=>C= ???

Decompilation Lab - What is inside?

If we start diging into implementation we will find an alias in Predef.Scala . So now will be a good time to mention what is Predef and what is an alias in Scala :)

type Function[-A, +B] = Function1[A, B]

For now ignore thise signs "- and +" next to letters A and B. Let's go into Function1 Declaration

@annotation.implicitNotFound(msg = "No implicit view available from ${T1} => ${R}.")
trait Function1[@specialized(scala.Int, scala.Long, scala.Float, scala.Double) -T1,
@specialized(scala.Unit, scala.Boolean, scala.Int, scala.Float, scala.Long, scala.Double) +R] 
extends AnyRef { self =>
  /** Apply the body of this function to the argument.
   *  @return   the result of function application.
   */
  def apply(v1: T1): R

  /** Composes two instances of Function1 in a new Function1, with this function applied last.
   *
   *  @tparam   A   the type to which function `g` can be applied
   *  @param    g   a function A => T1
   *  @return       a new function `f` such that `f(x) == apply(g(x))`
   */
  @annotation.unspecialized def compose[A](g: A => T1): A => R = { x => apply(g(x)) }

  /** Composes two instances of Function1 in a new Function1, with this function applied first.
   *
   *  @tparam   A   the result type of function `g`
   *  @param    g   a function R => A
   *  @return       a new function `f` such that `f(x) == g(apply(x))`
   */
  @annotation.unspecialized def andThen[A](g: R => A): T1 => A = { x => g(apply(x)) }

  override def toString() = "<function1>"
}

We can discuss shortly about some new construction from this code - (for example annotation specialized are interesting) but the purpose of this exercise is just to show structures and not to understand them at the first glance.

So to mark exercise as a successful you just need to know that there are some structures and that a function with just one parameter has it's dedicated type.

Soon we will implement methods andThen and compose by ourself but first let's do last one experiment.

Decompilation

  • Take look at class
class ClassWithAFunction {

  val fun:Int=>Int = x=>x+1

  def add(x:Int):Int = fun(x)
}
  • Compile 
projectpath$ sbt compile
  • Check generated classes
projectpath/target/scala-2.11/classes/jug/lodz/workshops/fp1$ ls lab -al

drwxrwxr-x 2 pawel pawel 4096 lut 21 09:53 .
drwxrwxr-x 5 pawel pawel 4096 lut 21 09:53 ..
-rw-rw-r-- 1 pawel pawel 1238 lut 21 09:53 ClassWithAFunction\$\$anonfun$1.class
-rw-rw-r-- 1 pawel pawel 1350 lut 21 09:53 ClassWithAFunction.class

So we can see that actually two files were generated. The first one ClassWithAFunction.class. Let's use standard Java Dissasembler to check what is inside :

https://docs.oracle.com/javase/7/docs/technotes/tools/windows/javap.html

And again detail of this dissasembled code are not important at this moment. The main point of this exercise is to take a quick glance how abstract functional world is connected with the real machine world.

  • Decompile
javap ClassWithAFunction.class


Compiled from "ClassWithAFunction.scala"
public class jug.lodz.workshops.fp1.lab.ClassWithAFunction {
  public scala.Function1<java.lang.Object, java.lang.Object> fun();
  public int add(int);
  public jug.lodz.workshops.fp1.lab.ClassWithAFunction();
}
  • Check the syntatic class :
javap ClassWithAFunction\$\$anonfun\$1.class 
Compiled from "ClassWithAFunction.scala"
public final class jug.lodz.workshops.fp1.lab.ClassWithAFunction$$anonfun$1 extends scala.runtime.AbstractFunction1$mcII$sp implements scala.Serializable {
  public static final long serialVersionUID;
  public final int apply(int);
  public int apply$mcII$sp(int);
  public final java.lang.Object apply(java.lang.Object);
  public jug.lodz.workshops.fp1.lab.ClassWithAFunction$$anonfun$1(jug.lodz.workshops.fp1.lab.ClassWithAFunction);
}

So really there is no sense to analyze what is apply$mcII$sp(int) - exercise is marked as success when participants understands that there are some additional classes generated and that there are tools to look inside if there is a need.

More about this : http://alvinalexander.com/scala/scala-class-to-decompiled-java-source-code-classes

Scala 2.12 should support java8 and InvokeDynamic instruction so most likely from version 2.12 this code will be simplified a lot and we will see java8 lambdas there

Homework

results matching ""

    No results matching ""